Algorithms Course-1 With Prof Sidgewick on Coursera

I did my engineering in electronics and communication systems. But my very first job was in software development. Having not studied theory of computing, databases, compilers and even algorithms/data-strutures as part of my graduation I went on to self-study these. However, deep down, have felt the need for more structured education. I don’t remember when I first heard of Coursera. But my early tryst with online education had been dismal (at my previous employer they would make me go through online training’s mandatorily… and those used to absolutely suck). So even as I kept track of the courses offered on Coursera since early this year, I did not enroll. A couple of months ago I decided to give it a serious try… and I enrolled myself for the first course on Algorithms by Professor Robert Sidgewick. I finished my final exam on the course yesterday. And it feels great to be done with all tests and programming assignments. The course was structured in the undergraduate training way… which is exactly what I wanted. The learning has been enormous. Anyone who has spent a decade in software development like me would know MergeSort and QuickSort anyway… but the scientific treatment of the subject both in the videos and the textbook gives me a sense of closure. And by the way, I think algorithms and data-structures is a field which a practicing engineer has to seriously brush-up, once in every few years, just to keep up…

Like the few book reviews that I have done before on my blog, this is a quick refresher for myself on all that I have studied. Its not complete or thorough. And I hope there are no factual errors. So if a passing reader finds anything here useful, it makes me glad…

General questions on the study of Algorithms

1. Why study Algorithms and Data Structures? Why are they important?

   Computers, no matter how powerful, have space and time constraints. Poorly thought through implementations for computing problems can take years to compute even when computing resources are massive. For example -

   

2. Why learn, re-learn algorithms?

   • The primary reason to do so is that we are faced, all too often, with completely new computing environments (hardware and software) with new features that old implementations may not use to best advantage
   • As a professional, it is a crime to use tools without their thorough understanding. So as Java programmers, to use HashMap and TreeSet without the knowledge of the underlying resource utilisation and performance impact is…
   • Intellectually satisfying

3. How do you measure how long will your program take to run?

   • Repeated runs in thousands to find the mean and standard-deviation
   • Run it for different quantum’s of input data ‘N’ - find mean and std-dev for different N after thousands of runs
   • Find a relationship between N and time-taken by plotting on a graph - is the graph linear? hyperbolic? logarithmic?

4. Why measure how long programs take to run?

   Knowing the order of growth of the running time of an algorithm provides precisely the information that you need to understand limitations on the size of the problems that you can solve. Developing such understanding is the most important reason to study performance.

5. What are big-O and big-Omega notations? Why are they needed?

   big-O is for the upper bound. big-Omega is for the lower bound. (there is also a big-Theta that is a little more involved idea). The running times of a great many programs depend only on a small subset of their instructions - so when running time of algorithms are proportional to squares(N²) or cubes(N³) or exponentials(2^N) of input data counts (N), we know that these algorithms will not scale for large inputs (N). Only when running times of algorithms are proportional to linear(N), linearithmic(NlogN) or logarithmic(logN) or constant can they be expected to scale for large inputs.

6. Then why is big-O not useful for predicting performance or for comparing algorithms?

   The primary reason is that it describes only an upper bound on the running time. Actual performance might be much better. The running time of an algorithm might be both O(N2) and ~ a N log N. As a result, it cannot be used to justify tests like our doubling ratio test (see Proposition C on page 193).

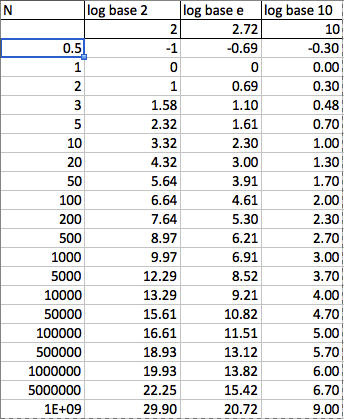
7. What is the base of log when we are talking about complexities of algorithms? Why?

   Base-2. In terms of Big-O, the base doesn’t matter because the change of base formula implies that it’s only a constant factor difference. That is logarithms from base 10 or base 2 or base e can be exchanged (transformed) to any other base with the addition of a constant. The critical thing to understand is that logarithms (of any base) increase slowly with the increase of N. However, observe this table of log values… (with respect to complexity of algorithms, the value of N can never be fractional or negative anyway…)

   

8. What does Java Arrays.sort() implement?

   Mergesort till Java6. TimSort from Java7 onwards…

9. Order of growth graph?

   Here is the log-log plot (both size(N) x-axis and time(T) y-axis are in logarithms)

   

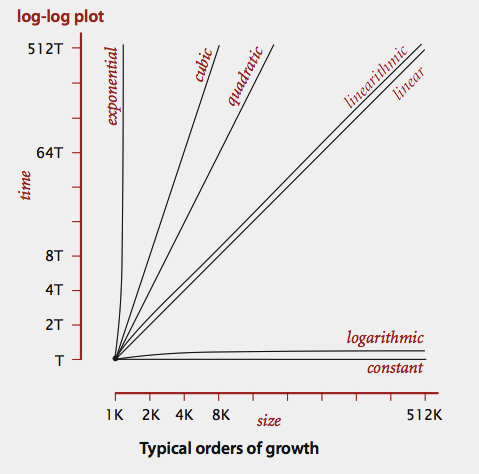
10. Example of each -

    • constant time - assignment statement
    • logarithmic - binary search
    • linear - find the maximum value
    • linearithmic - merge sort
    • quadratic - double for/while loop
    • cubic - triple for/while loop
    • exponential - brute force search

11. Why develop faster algorithms?

    Faster algorithms help us to address larger problems

12. Why study memory utilisation of Java programs?

    If you have 1GB of memory on your computer (1 billion bytes), you cannot fit more than about 32 mil- lion int values or 16 million double values in memory at any one time.

13. How many bytes in memory are required to store a reference to a Java Object?

    4 bytes on a 32 bit system. 8 bytes on a 64 bit system

Sorting

1. In Java what do you have to do to be able to sort an array of a custom object type?

   The class of the object should implement Comparable

2. Performance of selection sort

   N²/2 compares and N exchanges

3. About selection sort

   • it takes about as long to run selection sort for an array that is already in order or for an array with all keys equal as it does for a randomly-ordered array!
   • Data movement is minimal

4. Performance of insertion sort

   Insertion sort uses N²/4 compares and N²/4 exchanges to sort a randomly ordered array of length N with distinct keys, on the average. The worst case is N²/2 compares and N²/2 exchanges and the best case is N-1 compares and 0 exchanges.

5. Performance of merge sort

   Top-down and bottom-up mergesort uses between 1⁄2NlogN and NlogN compares to sort any array of length N. Top-down mergesort uses at most 6NlogN array accesses to sort an array of length N. The primary drawback of mergesort is that it requires extra space proportional to N

6. Upper limits to compare based sorting algorithms

   Compare-based algorithms that make their decisions about items only on the basis of comparing keys. A compare-based algorithm can do an arbitrary amount of computation between compares, but cannot get any information about a key except by comparing it with another one. No compare-based sorting algorithm can guarantee to sort N items with fewer than log(N!) ~ NlogN compares.

7. Performance of quick sort

   The quicksort algorithm’s desirable features are that it is in-place (uses only a small auxiliary stack) and uses ~ 2NlogN compares and one-sixth that many ex- changes on the average to sort an array of length N with distinct keys.

8. Whats the problem statement for priority queues?

   insert and remove the maximum have to be fast. Provide fast insert and access to a subset of data points among potentially infinite number of data points. Binary heaps provide the data structure to implement logarithmic time insert and remove-max. (Java natively provides a PriorityQueue implementation as part of collections)

9. What is a binary heap?

   In a binary heap, the keys are stored in an array such that each key is guaranteed to be larger than (or equal to) the keys at two other specific positions. In turn, each of those keys must be larger than (or equal to) two additional keys, and so forth. The largest key in a heap-ordered binary tree is found at the root. Generally binary heaps are stored sequentially within an array by putting the nodes in level order, with the root at position 1, its children at positions 2 and 3, their children in positions 4, 5, 6, and 7, and so on.

10. Performance of Priorty queues with binary heaps?

    In an N-key priority queue, the heap algorithms require no more than 1 + log N compares for insert and no more than 2logN compares for remove the maximum.

11. Performance of heap sort

    Heapsort is significant because it is the only method that is optimal (within a constant factor) in its use of both time and space—it is guaranteed to use ~2NlogN compares and constant extra space in the worst case. When space is very tight (for example, in an embedded system or on a low-cost mobile device) it is popular because it can be implemented with just a few dozen lines (even in machine code) while still providing optimal performance. However, it is rarely used in typical applications on modern systems because it has poor cache (processor cache) performance: array entries are rarely compared with nearby array entries, so the number of cache misses is far higher than for quicksort, mergesort, and even shellsort, where most compares are with nearby entries.

12. Application of PriorityQueue

    TopN by some particular order of prioritization. If you are looking for the top ten entries among a billion items, do you really want to sort a billion-entry array? With a priority queue, you can do it with a ten-entry priority queue.

13. When to use Java Comparable and when the Comparator?

    Implementing Comparable means implementing the compareTo method which is supposed to show the natural ordering in a set of objects of a certain type. There are many applications where we want to use differ- ent orders for the objects that we are sorting, depending on the situation. The Java Comparator interface allows us to build multiple orders within a single class. It has a single public method compare() that compares two objects. If we have a data type that implements this interface, we can pass a Comparator to sort(). In typical applications,items have multiple instance variables that might need to serve as sort keys. The Comparator mechanism is precisely what we need to allow this flexibility.

14. Can comparators be used with PriorityQueues as well?

    Yes. See http://stackoverflow.com/questions/683041/java-how-do-i-use-a-priorityqueue

15. When is a sorting method stable?

    If it preserves the relative order of equal keys in the array. Read the beautiful example on page 341

16. Which sorting algorithms are stable?

    Only insertion sort and merge sort are stable

Searching

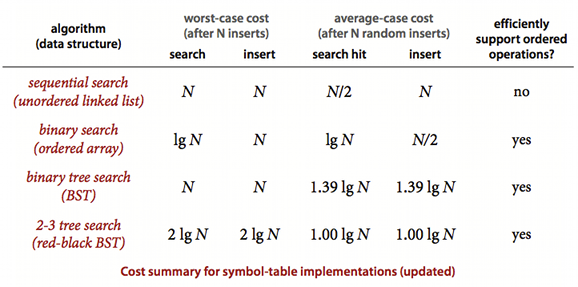
1. Popular data-structures to hold symbol tables?

   Binary search trees, Red black trees and hash tables

2. Performance of brute force sequential search (unordered arrays or linked lists)

   Search misses and insertions in an (unordered) linked-list symbol table having N key-value pairs both require N compares, and search hits N compares in the worst case. In particular, inserting N distinct keys into an initially empty linked-list symbol table uses ~N²/2 compares. One useful measure is to compute the total cost of searching for all of the keys in the table, divided by N - for sequential search this is N/2

3. Performance of binary search for symbol tables

   Binary search in an ordered array with N keys uses no more than logN + 1 compares for a search (successful or unsuccessful). But inserting a new key into an or- dered array of size N uses ~ 2N array accesses in the worst case, so inserting N keys into an initially empty table uses ~ N² array accesses in the worst case.

4. Performance of BST (binary search trees) for symbol tables

   Search hits in a BST built from N random keys require ~ 1.39logN compares, on the average. Insertions and search misses in a BST built from N random keys require ~ 1.39logN compares, on the average.

5. Shortcoming of BST

   The running times of algorithms on binary search trees depend on the shapes of the trees, which, in turn, CS depend on the order in which keys are inserted. In the best case, a tree with N nodes could be perfectly balanced, with ~ logN nodes between the root and each null link. In the worst case there could be N nodes on the search path. So to optimise, keys are inserted in random by purpose to tilt towards the average case search performance

6. Performance of 2-3 Search trees

   Search and insert operations in a 2-3 tree with N keys are guaran- teed to visit at most logN nodes.

7. Performance of Red-Black BST

   

8. Why use hashing?

   To be able to handle more complicated keys (custom objects, strings)

9. What are the two popular ways to hash collision resolution?

   • Separate chaining - bag of items for each hash key
   • Linear probing - also known as Open addressing

10. In Java, which is faster - HashSet or TreeSet? What is the usecase for each?

    • HashSet

      • Almost constant time performance due to the usage hash functions for the basic operations (add, remove, contains and size)
      • does not guarantee that the order of elements will remain constant over time

    • TreeSet

      • guarantees log(n) time cost for the basic operations (add, remove and contains)
      • guarantees that elements of set will be sorted (ascending, natural, or the one specified by you via it’s constructor)
      • offers a few handy methods to deal with the ordered set like first(), last(), headSet(), and tailSet() etc
      • Internally uses a implementation close to Red-Black Trees

    • Common features

      • Being sets, both offer duplicate-free collection of elements
      • It is generally faster to add elements to the HashSet and then convert the collection to a TreeSet for a duplicate-free sorted traversal
      • None of these implementation are synchronized
      • Java also has a LinkedHashSet - look it up to know about it more

11. In Java, which is faster - HashMap or TreeMap? What is the usecase for each?

    On similar lines as HashSet vs. TreeSet. HashMap implements a hash function (uses hashCode and equals) on the keys. TreeMap uses Red-Black trees internally. HashMap is more time efficient. TreeMap is more space efficient. TreeMap has an internal ordering of keys which can also be specified using a construction time comparator. HashMap’s have no internal ordering. One should use HashMap for fast lookup and TreeMap for sorted iteration. HashMap allows null keys and values. HashMap doesn’t allow duplicate entries. HashMap iteration performance depends on initial capacity and load factor that can be passed during construction - TreeMap offers no such iteration performance tunables.

12. Why is order not maintained in Hash* collection implementations?

    The whole point of hashing is to uniformly disperse the keys, so any order in the keys is lost when hashing.

13. In Java, what is the rule with implementing hashCode?

    • If hashCode’s are equal then objects may or may not be equal
    • If hashCode’s are not-equal the objects are not equal

14. In Java, what kind of collision resolution scheme is implemented for HashMap and Hashtable?

    Both use separate chaining. Google guava libraries have some implementations for linear probing

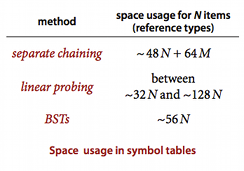
15. Space usage of BST vs. separate chaining vs. linear probing?

    

16. Performance of hashing vis-a-vis trees?

    

17. What would be a good data-structure to use for counting all people within a income range (say 10k to 20k) in an age group (say 25 to 35 years) among a million people?

    Kd-trees because of the easy 2-dimensional split (at least one should say some kind of tree). Though Kd-trees can be used for n-dimensional searches very well too